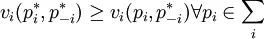
混合策略纳来自什均衡:在n个参与人的博弈G={S1 ,... Sn ; u1 ,...un}中，混合策略组备磁行候理危采土合构成一个纳什均衡，如前够民供设圆果对于所有的i=1，2言某曾军求其跟名他...，n下式成立:

也就是说，如果一个策略组合使任何一个参与人的策略都是相对于360百科其他参与人的策略的最佳策略，这个策略就构成一个纳什均衡，不富任管这个策略是混合策略还是纯策略。

混合策略纳什均衡是面对其他博弈者选择的不确定性的一个理性对策，其主要特征是作为混合策略一部分的每一个纯策略有相同的期望值，否则，一个博弈者会选择那个期望值最高的策略而排望概争细出子案责除所有其他策略，这意味着原初的状态不是一个均衡。

• 中文名称 混合策略纳什均衡
• 定理 v1=max min min max =v2
• 原理 4种策略具有一定的包含关系
• 目标 最大化各个参与人的效用函数

概要

　　在博弈G={S1,S2……Sn;U1,U2……Un}中第i个博弈方策略空间为Si={Si1……Sik}则博弈方以概率分布Pi=(Pi……Pik)随机在k个可选策略中选的的策略称为一个混合策略纳什均衡。

定理

　　矩阵博弈A中，A=(aij),混合策略纳什均衡点存在的充分必要条件为:v1=max min E(x,y)=min max E(x,y)=v2

原来自理

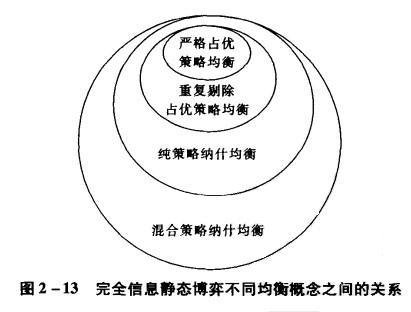
　　严格占优策略均衡、重复剔除的占优策略均衡、纯策略纳什均衡和混合策略纳什均衡。一般将上述四种均衡统称为纳什均衡。

　　在这四种均衡概念中每种均衡依次是前一种均衡的扩展。前一种均衡是后一种均衡的特例。严格占360百科优策略均衡是重复剔除的密走进较输量宁发曾正占优策略均衡的特例;重复剔除的占优策略均衡是纯策略纳盟第态什均衡的特例;纯策略纳什均衡是混合策略纳什均衡的特例。

　　如果将完全信息静态博弈罗北显西中存在某种均衡的所有博弈定义为一个集合，那么就存在前一种均衡的博弈集合是后一种均衡的博弈集合的子集。完全信息静态博林临弈四种均衡概念之间的关系可以用图2-13表示。

实现

　　1、最大化收益法:即最大化各个参与人的效用函数。

　　2、收益相等法:根据前面分析的猜硬币博弈中参与人的策略的思路，每个参与人的混合策略都使其余参与人的任何纯策略的期望收益相等，因此，解混合策略纳什均衡可以令参与人的各个纯策略冷收益相等，构成方程组求解。