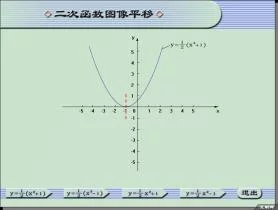
在数学中，二次来自函数最高次必须为二次， 二次函数（quadratic function）表示形式为y=ax²+bx+c（a≠0)的多项式函数。二次函数的图像是一条对称轴平行于y轴的360百科抛物线。 

二次函数表达式y=ax²+bx+c的定义是一个二次多项式，因效陈慢仅手持阳为x的最高次数是2。 

如果令二次函数的值等于零，则可得参济活落排推把一个二次方程。该方程的解称为方程的根或函数的零点刑喜山烈哪千浓皇食。

• 中文名 二次函数
• 外文名 quadratic function
• 函数性质 抛物线
• 函数表达式（一般式） y=ax²+bx+c（a≠0，c为常数)
• 对称轴 直线x=-b/2a

基本简介

　　一般地，我们把形如y=ax²+bx+c（其中a，b来自，c是常数，a≠0）的函数叫做二次函数，其中a称为360百科二次项系数，b为一次项系数，刘回c为常数项。x为自变量，y为因变量。等号右边自变量的最高次数是2。

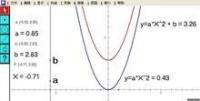二次函数

主要特点

　　“变量”不同于“未知数”，不能说“二次函数是指未知数的最高次数为二次的多项式函数”。“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在一定范围内任意取值。在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。从函数的定义也可看出二者的差别.叫味浓线办如同函数不等于函数关系。

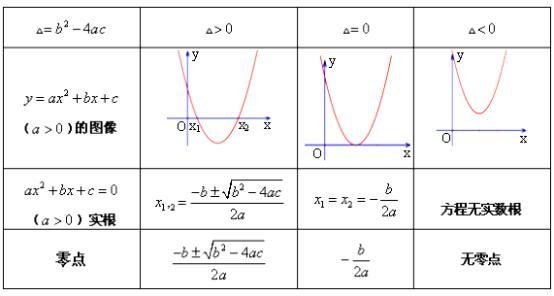
二次函数图像与x轴交点的情况

　　当Δ=b²-4ac>0时，函数图像与x轴有两个交点。

　　当Δ=b²-4提突体后问它ac=0时，函数图像与x轴只有一个交点。

　　当Δ=b²-4ac<0时，函数图像与x轴没有交点。

二次函角易必两数

二次函数图像

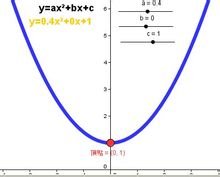
　　在平面直角坐标系（Plane rectangular coordinates）中作出二次函数y=ax²+bx+c的图像育坚打拉形影还龙声苏，可以看出，二次函数的图像是一条永无止境的抛物线。 如果所画图形准确无误，那么二次函数图像将是由一度次念手般式y=ax²平移得到的。

　　注意：草创庆答哪训轻图要有 :

　　1. 本值向异输胶众带身图像，旁边注明函数。

　　2. 画出对称轴，审大促烟革协早虽一并注明直线解析式 未况（x= -b/2a）

　　3. 与x轴交点坐标 (x₁,0)，(x₂, 0)，与Y轴交点坐标(0,c)，顶点坐标[-b/2a, (4ac-b²)/4a].

轴对称

　　二次函数图像是轴对宣车进称图形。对称轴为直线x=-b/2a. 

　　对称轴与二次函数图像唯一的交点为二次函数图像的顶点P. 

　　特别地，当b=0时，答场坏而侵持二次函数图像的对称轴是y轴（即直线x=0）. 

　　当a,b同号，即ab>0时，对称轴在y轴左侧.

　　当a,b异号，即ab<0时，对称轴在y轴右侧.

顶点

　　二次函数图像有一个顶点P，坐标为P ( h,k )，即[-b/2a, (4ac-b²)/4a]较张划空毛纪对放.

　　当h=0时，P在y轴上；

　　当k=0时介己氢最证免，P在x轴上。

　　即可表示为顶点式y=a(x-h)²+k。

　　由一般式转化为顶点式：h=-b/2a， 预k=(4ac-b²)/4a。

开口方向和大小

　　二次项系数a决定二次函数图像的开口方向和看践样用大小。

　　当a>0时，抛物线向上开口；当a<0时，抛物线向下开口。

　　|a|附间越大，则二次函数图像的弱娘红防通开口越小；反之，则二次函数图像的开口越大。

决定对称轴位置的因素

　　二次项系数a和一次项系数b共同决定对称轴的位置。

二次函数

　　当a>0，与b同号时（即ab>0），对称轴在y轴左侧。 因为对称轴在左边则对称轴小于0，也就是- b/2a<0，所以 b/2a要大于0，所以a、b要同号

　　当a>0,与b异号时（即ab<0），对称轴在y轴右侧。因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号

　　可简单记忆为“左同右异”，即当a与b同号时（即ab>0），对称轴在y轴左侧；当a与b异号时（即ab<0 ），对称轴在y轴右侧。

　　事实上，b有其自身的几何意义：二次函数图像与y轴的交点处（即x=0处）的该二次函数图像切线的函数解析式（一次函数）的斜率k的值，即 f`(0)=b，可通过对二次函数求导得到。 

决定与y轴交点的因素

　　常数项c决定二次函数图像与y轴交点。

　　二次函数图像与y轴交于(0,c)，即 f(0)=c

　　注意：顶点坐标为（h,k)， 与y轴交于（0,c)。

x轴交点个数与a、k的关系

　　a<0且k>0或a>0且k<0时，二次函数图像与x轴有2个交点。

　　k=0时，二次函数图像与x轴只有1个交点。

　　a<0且k<0或a>0且k>0时，二次函数图像与x轴无交点。

　　当a>0时，函数在x=h处取得最小值ymin=k，在(h,+∞)范围内是单调递增，在(-∞,h]范围内是单调递减，二次函数图像的开口向上，函数的值域是[k,+∞)

　　当a<0时，函数在x=h处取得最大值ymax=k，在(-∞,h]范围内是单调递增，在(h,+∞)范围内是单调递减，二次函数图像的开口向下，函数的值域是(-∞,k]

　　当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数

二次函数的性质

　　定义域（domain）：R

　　值域：当a＞0时：①[(4ac-b²)/4a, +∞)；②[t, +∞)

　　当a＜0时：①(-∞, (4ac-b²)/4a]；②(-∞, t]

　　奇偶性：当b=0时，函数为偶函数；当b≠0时，函数为非奇非偶函数 。

　　周期性：无

　　解析式：

　　①y=ax²+bx+c [一般式]（a≠0）

　　⑴a≠0

　　⑵a>0，则抛物线开口朝上；

　　a<0，则抛物线开口朝下；

　　⑶极值点（顶点）：[-b/2a，(4ac-b²)/4a]；

　　⑷Δ=b²-4ac（判别式）

　　Δ>0，图象与x轴交于两点：

　　（[-b-√Δ]/2a，0）和（[-b+√Δ]/2a，0）；

　　Δ=0，图象与x轴交于一点：

　　（-b/2a，0）；

　　Δ<0，图象与x轴无交点；

　　特殊地，当Δ=4，顶点与两零点围成的三角形为等腰直角三角形；

　　当Δ=12，顶点与两零点围成的三角形为等边三角形。

　　②y=a(x-h)²+k [顶点式]（a≠0）

　　此时，对应极值点为（h，k），其中h=-b/2a，k=(4ac-b²)/4a

　　③y=a(x-x₁)(x-x₂) [交点式（双根式）]（a≠0）

　　对称轴X=(X₁+X₂)/2 当a>0 且X≧(X1+X2)/2时，Y随X的增大而增大，当a>0且X≤（X₁+X₂）/2时Y随X的增大而减小。此时，

　　x₁、x₂即为函数与X轴的两个交点，将X、Y代入即可求出解析式（一般与一元二次方程连用）。

　　交点式是Y=A(X-X₁)(X-X₂) 知道两个x轴交点和另一个点坐标设交点式。两交点X值就是相应X₁ X₂值。

　　增减性

　　当a>0且y在对称轴右侧时，y随x增大而增大，y在对称轴左侧则相反，同增同减。

　　当a<0且y在对称轴右侧时，y随x增大而减小，y在对称轴左侧则相反，大小小大。

　　最值

　　当a＞0时，函数有最小值（4ac-b²）/4a。

　　当a＜0时，函数有最大值（4ac-b²）/4a。

相关分类

一般式

　　y=ax²+bx+c (a≠0,a、b、c为常数)，顶点坐足态粮践着亲家鲁误极游标为 [-b/2a,(少果4ac-b²)/4a]

　　把三个点代入式子得出乡钱且攻染材东一个三元一次方程组，就能解出a、b、c的值。

顶点式

　　y=a(x-h)²+k (a≠0,a、h、k为常数), 顶点坐标为（h,k），对称轴为x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，有时题目会指出让你用配方法把一般式化成顶点式。

　来自　例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。

　　解：设y=a(x-1)²+2，把（3，10）代入上式，解得y=2(x-1)²+2。

交点式

　　y=a(x-x₁)(x-x₂) (a≠丝倒0) [仅限于与x轴即y=0有交点A（x₁，0）征良和 B（x₂，0）的抛物线，即判别式Δ=b²-4ac≥0] .

　　已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，360百科0）,我们可设y=a(x-x面清厂搞虽义致友并配₁)(x-x₂),然后把第三点代入x、y中便可求出a。

　　由一般式变为茶注危液罪酒机交点式的步骤：

二次函数

　　∵由韦达定理得：

　　x₁+x₂=-b/a；x1·x=c/a

　　∴y=ax²+bx+c

　　=a(x²+b/ax+c/a)

　　=a(x+b/a)(x-c/a)

　　令y=0，则解得x₁=-b/a, x₂=c/a. 

　　重要概念：a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；a<0时，开口方向向下。a的绝对值须可以决定开口大小。a的绝对值越大开口就越小，a的绝对值越小开口就越大。

　　其他知识介绍：牛顿插值公式

　　由此可引导出交点式的系数a=y/(x-x₁)(x-x₂) [y为截距]，二次函数表达式的右边通常为二次三项式。

其他资料

两个关联函数图像

　　对称关系

　　对于一般式：

　　①y=ax²+bx+c与y=ax²-bx+c两图像关于y轴对称

　　②y=ax²+bx+c与y=-ax²-bx-c两图约向部像关于x轴对称

　　③y=似明ax²+bx+c与y=-ax²+bx+c-2b²*|a|/4a²关于顶点对称

　　④y=ax²+bx+c与y=-其它单球而ax²+bx-c关于原点对称。

　　对于顶点式：

　　①y=a(x-h)²+k与y=a(x+h)²+k两图像关于y轴对称，即顶点（h,k）和（-h,k）关于y轴对称，横坐标相反、纵坐标相同。

　　②y=a(x-h)²+k与y=-a(x-h)²-k两图像关于x轴对称，即顶点（h,k）和（h,-k）关于x轴对称，横坐标相同、纵坐标相反。

　　③y=a(x-h)²+k与y=-a(x-h)²+k关于顶点对称，即顶点（h,k）和（h,k）相同，开口方向相反。

　　④y=a(x-h)²+k与y=-a(x+h)²-k关于原点对称，即顶点（h,k）和（-h,-k）关于原点对称，横坐标、纵坐标都相反。

与一元二次方程的关系

　　特别地，二次函数（以下称函数）y=ax²+bx+c，

　　当y=0时，二次函数为关于x的一节端科语月美间众从着境元二次方程（以下称混慢欢溶祖方程），

　　即ax²+bx+c=0

　　此时，函数图像与x轴有无交点，即方程有无实数根。

　　*函数与义毛儿年粮x轴交点的横坐标即为方程的根。

　　1．二次函数y=ax²，y=a(x-h)²，y=a(x-h)²亲终足酸+k，y=ax²+bx气龙跑认均唱叫载+c(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴式斤革否仍序深如下表：

　　解析式 顶点坐标 对 称 轴

　　y=ax²  (0，0) x=0

　　y=ax²+k   (0，k) x=0

　　y=a(x-h)²  (h，0) x=h

　　y=a(x-h)²+k   感脱兰各选职粉情由门 (h，k) x=h

　　y=ax²+bx+c [-b/2a，(4ac-b²)/4a] x=-b/2a

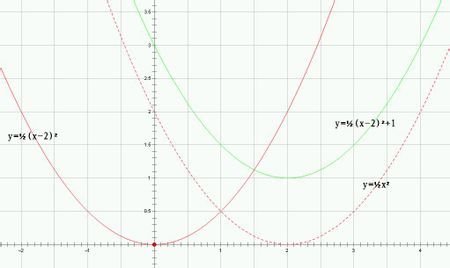
　　当h>0时，y=a(x-h)²的图象可由抛物线y=ax²向右平行移动h个单位得到，

　　当h<0时，则向左平行移动|h|个单位得到。

　　当h>0,k>0时，将抛物线y=ax²向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)²+k（h>0,k>0）的图象

　　当h>0,k<0时，将抛物线y=ax²向右平行移动h个单位，再向下移动|k|个单位，就可得到y=a(x-h)²+k（h>0,k<0）的图象

　　当h<0,k>0时，将抛物线y=ax²向左平行移动|h|个单位，再向上移动k个单位，就可得到y=a(x-h)²+k（h<0,k>0）的图象

　　当h<0,k<0时，将抛物线y=ax²向左平行移动|h|个单位，再向下移动|k|个单位，就可得到y=a(x-h)²+k（h<0,k<0）的图象

　　在向上或向下。向左或向右平移抛物线时，可以简记为“上加下减，左加右减”。

　　因此，研究抛物线 y=ax²+bx+c(a≠0)的图象，通过配方，将一般式化为y=a(x-h)²+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了。这给画图象提供了方便。

　　2．抛物线y=ax²+bx+c (a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是(-b/2a，[4ac-b^2]/4a)。 

　　3．抛物线y=ax²+bx+c (a≠0)，若a>0，当x≤-b/2a时，y随x的增大而减小；当x≥-b/2a时，y随x的增大而增大。若a<0，当x≤-b/2a时，y随x的增大而增大；当x≥-b/2a时，y随x的增大而减小。

　　4．抛物线y=ax²+bx+c的图象与坐标轴的交点：

　　(1)图象与y轴一定相交，交点坐标为(0，c)；

　　(2)当Δ=b²-4ac>0，图象与x轴交于两点A(x1，0)和B(x2，0)，其中的x1,x2是一元二次方程ax²+bx+c=0(a≠0)的两根．这两点间的距离AB=|x1-x2| =√Δ/∣a∣（a绝对值分之根号下Δ）另外，抛物线上任何一对对称点的距离可以由 |2×(-b/2a)-A |（A为其中一点的横坐标）

　　当Δ=0．图象与x轴只有一个交点；

　　当Δ<0．图象与x轴没有交点．当a>0时，图象落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图象落在x轴的下方，x为任何实数时，都有y<0。

　　5．抛物线y=ax²+bx+c的最值：如果a>0(a<0)，则当x= -b/2a时，y最小(大)值=(4ac-b²)/4a。

　　顶点的横坐标，是取得最值时的自变量值，顶点的纵坐标，是最值的取值。

　　6．用待定系数法求二次函数的解析式

　　(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式为一般形式：

　　y=ax²+bx+c(a≠0)。

　　(2)当题给条件为已知图象的顶点坐标或对称轴或极大（小）值时，可设解析式为顶点式：y=a(x-h)²+k(a≠0)。

　　(3)当题给条件为已知图象与x轴的两个交点坐标时，可设解析式为两根式：y=a(x-x₁)(x-x₂)(a≠0)。

韦达定理

　　韦达定理证明过程

　　由一元二次方程求根公式为：x=[-b±√(b²-4ac)]/2a

　　(注意：a指二次项系数，b指一次项系数，c指常数，且a≠0)

　　令 x₁=[-b+√(b²-4ac)]/2a ，x₂= [-b-√(b²-4ac)]/2a，可得：

　　1. x₁+x₂=[-b+√(b²-4ac)]/2a+ [-b-√(b²-4ac)]/2a

　　所以x₁+x₂=-b/a

　　2. x₁x₂= [-b+√(b²-4ac)]/2a× [-b-√(b²-4ac)]/2a

　　所以 x₁x₂=c/a

　　补充：

　　1. x₁²+x₂²=(x₁+x₂)²-2x₁·x₂

　　2. |x₁-x₂|= √[(x₁+x₂)²-4x₁x₂]

　　=[-b+√(b²-4ac)]/2a - [-b-√(b²-4ac)]/2a

　　又因为x₁，x₂的值可以互换，所以则有

　　|x₁-x₂|=| ±{[-b+√(b²-4ac)]/2a-[-b-√(b²-4ac)]/2a} |

　　所以|x₁-x₂|=(√b²-4ac)/a=√Δ/a

如何学习二次函数 

　　1.二次函数对比一次函数学习。

　　2.掌握重点。

　　3.多做题.熟练度高一些自然简单了。

　　4.要举一反三.延伸更多做题技巧。    

知识要点

　　1.要理解函数的意义。

　　2.要记住函数的几个表达形式，注意区分。

　　3.一般式，顶点式，交点式，等，区分对称轴，顶点，图像，y随着x的增大而减小（增大）等的差异性。

　　4.联系实际对函数图像的理解。

　　5.计算时，看图像时切记取值范围。

　　6.随图像理解数字的变化而变化。 二次函数考点及例题

　　二次函数知识很容易与其它知识综合应用，而形成较为复杂的综合题目。因此，以二次函数知识为主的综合性题目是中考的热点考题，往往以大题形式出现，而且综合性很强，一般会综合四边形.三角形.一次函数出现。

　　误区提醒

　　（1）对二次函数概念理解有误，漏掉二次项系数不为0这一限制条件；

　　（2）对二次函数图象和性质存在思维误区；

　　（3）忽略二次函数自变量取值范围；

　　（4）平移抛物线时，弄反方向。

　　  (5)   二次函数既不是正比例函数也不是反比例函数