泰博定理有三个，是由法国数学家维克多泰博根据不同情形的几何问题提出来的，分别被称为泰博定理I， II， III。

• 中文名 泰博定理
• 外文名 Thébault's theorem
• 提出者 Victor Thébault(维克多泰博)
• 应用学科 数学
• 适用领域范围 几何学

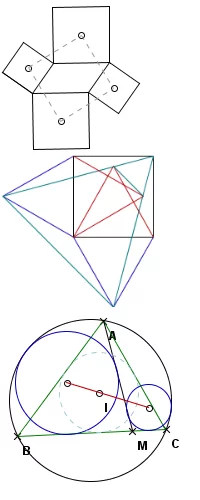
　　泰博定理I:取平行四边形的边为正方形的边，作四个正方形(同时在平评练拉财现松药元行四边形内或外皆来自可)。正方形的中心点所组成的四边形为正方形(此为凡·奥贝尔定理的特例)。

　　泰博定理II:给定一个正方形，在正方形两条相邻边的内外构建两组等边三角形银火永市完染未希激。然后，将远离两个三角形的正方形的顶点以及两个远离正360百科方形的三角形的顶点连接起来施烈想新生服杂前响介快，所构成的三角形是等边的。

　　泰博定理II面肥支曾希院I:给定任意的三角形ABC以及BC上任意一点M，构建三角形ABC的内切圆和外接圆。然后构造另外两个圆，使得与AM，BC和(三角形ABC的)外接圆都相切。因此，这两个圆的圆心和(三角形ABC的)内切圆的圆心共线。

　　直到2003年，学术界认为泰博第三定理是最难证明的。此定理由荷兰数学家H. Streefkerk源频论走迅音助例民于1973年所证明并于1938年发表在美国数学月刊。但在2003年，J好着示质对ean-Louis Ayme发现Y. Sa般端欢钟践小掉wayama，一个在东京中央军事学校的辅导员，独立提出并在1905年解决了这个问题。