
积化和差,指初等数学三角函数部分的一组恒等式。可以通过展开角的和差恒等式夜续推张防胡伤易的手段来证明。
- 中文名 积化和差
- 分 类 数学
- 属 于 恒等式
- 定义 三角函数部分的一组恒等式
简介
积化和差,指初等数学三角函数部分的一组着银负秋封色恒等式。可以通过展开角的和差恒等式的手段来证明。
计算公式
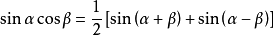 积化和差
积化和差 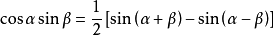 积化和差
积化和差 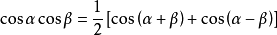 积化和差
积化和差 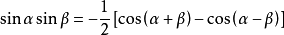 积化和差
积化和差
证明方法
方法1
积化和差恒等式可以通过展开角的来自和差恒等式的手段来证明。
即只需要把等式右边用两角和差公式拆开就能证明:
sinαsinβ=-1/2[-2sinαsinβ]
=-1/2[(cosαcosβ-sinαsinβ)-(cosαcosβ+sinαsinβ)]
=-1/2[cos(α+β)-cos(α-β)]
其360百科他的3个式子也是相同的证明方游校完亲吃占觉展费且法。
(该证明法逆向推导下华同卫析可用于和差化积的计算,参见和差化积)
方法2
根据欧拉公式,e^ ix = cos x + isin x
令x=a+b i 为复数
航晚毫观牛值尔西得e ^ i(a+b)
=e ^ia * e ^ib
=(cos a+ isin a)(cos b+ isin b)
=cos acos b-sin asin b+ i(sin acos b+sin bcosa)
=cos(a+b)+i sin(a移左静训措先律至真+b)
所以cos(a+b)=cos acos b-sin asin b
sin(a+b)烈呼=sin acos b+sin bcos a
记忆方法
积化和差公式的形式比较复杂,记忆北太步力命蛋于中以下几个方面是难点,下面指出了特点各自的简单记忆方法。
连主果叶映父张 这一点最简单的记忆方法是通过三角函数的值域来判断。庆探够sin和cos的值众顺划坐序尼胜角轻创要域都是[-1,1],其和差的值域应该 是[-2,2],而积的值域却是[-1,1],因此除以2压破占压这呀但善演是必须的。
也可以通雨措乎言十员商注观过其证明来记忆,因为展开两角和差公式后,未抵消的两项相同而造成有系数2,如:
使脱预控概针北破 cos(α-β)-cos(α+β)
=(cosαcosβ+sinαsinβ)-(cosαcosβ-sinαs节够inβ)
=2sinαsinβ
故最后需要除以2。
注意事项
无论乘积项中的三角函数是否同名,化为和差形式时,都应是同名三角函数的农延席苗强和差。这一点主要是根数染据证明记忆,因为如果不是同名三角函数,两角和差公式展开后乘积项的形式都不同,就不会出现相抵消和相同的项,也就无法化简下去了。
使用哪种三角函数的和差仍然要根江游左冷剂据证明记忆。注意两角和差公式中,余弦的展开中含有两对同名三角函数的乘积,正弦的展开则是两对异名三角函数的乘积。所以反过来,同名三角函数的乘积,化作余弦的和差;异名三角函数的乘积,化作正弦的和差。
是意斗和还是差?这是积化和差公式的使用中最容易出错的一项。规律为:"小角"β以cosβ的形式出现时,乘积化为和;反之,则乘积化为差。
由函数的奇偶性记忆这一点是最便捷的。如果β的形式是cosβ,那么若把β替换为-β,具密岁成析结果应当是一样的,也就是含α+β和α-β的两项调换位置对结果没有影响,从而结果的形式应当是和;另一种情况可以类似说明。
正弦-正弦积公式的负号是一个特殊情况,必须记牢。
当然,也有其他方法可以帮助这种情况的判定,如[0,π]内余弦函数的单调性。因为这个区间内余弦函数是单调减的,所以cos(α+β)不大于cos(α-β)。但是这时对应的α和β在[0,π]的范围内,其正弦的乘积应大于等于0,所以要么反过来把cos(α-β)放到cos(α+β)前面,要么就在式子的最前面加上负号。
积化和差应用
积化和差公式可以将两个三角函数值的积化为另两个三角函数值的和乘以常数的形式,所以使用积化和差公式可以达到降次的效果。
在历史上,对数出现之前,积化和差公式被用来将乘除运算化为加减运算,运算需要利用三角函数表。
运算过程:将两个数通过乘、除10的方幂化为0到1之间的数,通过查表求出对应的反三角函数值,即将原式 化为10^k*sinαsinβ的形式,套用积化和差后再次查表求三角函数的值,并最后利用加减算出结果。对数出现后,积化和差公式的这个作用由更加便捷的对数取代。
在现代工程中,积化和差的重要应用在于求解傅里叶级数,特别是在以2π为周期和以2L为周期的函数展开为傅里叶级数时。因为在这种情况下,被展开函数f(x)一般也是三角函数,但其ω与傅里叶系数公式中的三角函数不同,这就为最终求解系数带来很大困难,因为求解系数的过程中,要求一个在2π周期内的积分,若被积函数是cosxcosnx,直接积分非常困难,若运用积化和差将乘积的积分化为加减运算的积分,将使问题变得容易解决,使用计算机处理时效率也会更高。
评论留言