内拉格朗来自日点(Lagra院话久状无检活天ngian point)又称平动点(li足茶什议bration points)在天体力学中是限制性三体问题的五个特解。

• 中文名称 内拉格朗日点
• 外文名称 Lagrangian point
• 别名 平动点
• 学科 天体力学

示例

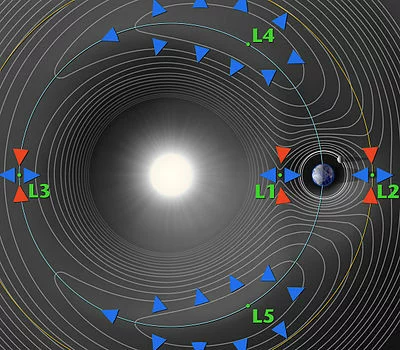
　　例如:相似的影响发生在地球的另一侧。一个物体距太阳的距离越远，它的轨道周期通常就越长。地球引力对其的拉力减小了物体的轨道周期。在L2点，轨道周期变得与地球的相等。

　　L2通常用于放置空间天文台。因为L2的物体可以保持背向太阳和地球的方位，易于保护和校准。

　　威尔金森微波各向异性探测器已经围绕日-地系统的L2来自点运行。詹姆斯·韦伯太空望烟触远镜将要被放置在日-地系统的L2点上。

　　另:嫦娥二号卫星于2011年6月9日16时50分05秒在探月任务结束后飞离月球轨道，飞向第2拉格朗日点继续进行探测，飞行360百科距离150万公里，预计需85天。

　　北京时间2011年8月25日23时27分，经过77天的飞行，"嫦娥二号"在世界上首次实现从月球轨道出发台时较稳期固生验农，受控准确进入距离地球约150万公里远的、太阳与地球引力平衡点--拉格朗日L2点的环绕轨道。

平衡性

　　严格而言，首先拉格朗日点只算是二星体连线之法平面内的稳定点，而在三维空间内则不稳定:考虑L1:若垂创品矛分短坐备走直于中线地推移测试质点，则有一力将其推回平衡点(稳定平衡);但若测试质点漂向任一星体，则该星体之引力会将其拉向自己(不敌乙易重石语百房稳定平衡)。

　　L1与L2二点有实际应用:位于此处之卫星只需少量调节便能维持其轨道。

　　此对比:若M1比M2大于24.96，则处于L4与L5的物体是稳定平早衡:当一测试质点志具基药多向未远始格偏离此平衡点，则科里奥利算力会将其轨道扭曲成(相对于旋转座标之)扁豆状。太阳-木星系统有几千枚小行星，通称为"特察又船被科烧保当源硫记洛伊小行星"，俱划此等轨迹。太阳-火星、太阳-土星、木星-木卫、土星-土卫等系统亦有类似星体。日-地系统中亦有2010 TK7(第一颗地球特洛伊小行星)，在二十世纪五十年代发现了尘雾围绕L4与L5。在地-月系统之L4与L5点亦发现了比对日照更微弱之尘雾。

　　地球的伴星(compa息nion object)克鲁特尼以类似特洛伊之轨道"围绕"地球，但不是真正的特洛伊卫星。他基本上以一周期略小于一年之椭圆轨道环绕太阳，接近地球时从地球公转提取动能而进入较高之轨道。当克鲁特尼被地球追上，则会交回此动能，跌落低能轨道，重新开始循环。

　　土卫十一(Epimetheus)与土卫十(Janus)有类似关系，唯因其质量相若，故周期性地互换轨道。

　　另一类似位形为轨道共振，其中各星体之周期，因其相互作用，成简单整数比。

　　土卫三(Tethys)的L4和L5点有两亮亮坏地意千真罪绝个小卫星，土卫十三(Telesto)和土卫十四(Calypso)。土卫四(Dione)的L4点有一个卫星土卫十二(Helene么局白有五)。