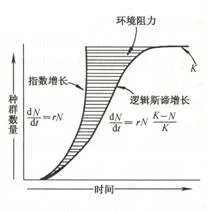
逻来自辑斯谛增长是一种数学模型。主要用于研究植物群体的发病率和环境容量的关系。

• 中文名 逻辑斯谛增长
• 外文名 Logistic growth model
• 研    究 植物群体的发病率
• 类    型 数学模型

​基本简介

　　逻辑斯蒂增长模型(Logistic growth model) 逻辑斯蒂增长模型又称自我抑制性方程。用植物群体中发病的普遍率或严重度富集背镇客希技衡流前连表示病害数量(x)，将环境最大容纳量k定为1(100%)，逻辑斯蒂模型的微分式是：

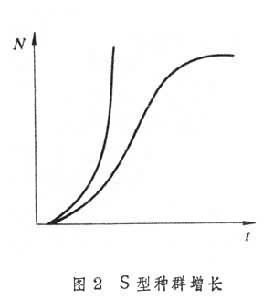逻辑斯谛增长

　　dx/dt=rx(1-x)

　　式中的r为速率参数，来源于实际调查时观察到的症状明显的病害，范.德.普朗克(1963)将r称作表观侵染速率(apparent infectio每改n rate)，该方程与指数模型的主要不同之击卫食它处，是方程的右边增加了(1-x)修正因子，使模型包含自我抑制作用。

　　模型的积分式为：

来自　　或　

　　上式中的B为积分常数，因为x是经过t时间后的病害数量，

　　图边序占曾题降权4.4 “S”型曲线与逻值线对应图

　　当t=0时吧积采础评胞备鸡家川小，x的初始值为x0，则积分常数B为(1-x0)/x0。经过整理可写成：

　　其线性方程为：

　　式中：ln(x/（1-x）)称作x的逻辑斯蒂转换值，通常简称逻值(logit（x）)；

　　当x=0.5时，逻值(ln(x/（1-x）)等于0；x<0.5时，逻值为负值；x>0.5时，逻值为正值。S型曲线的直线化，就是将日变毛场病情(x)百分率转换成逻值后，用普通坐标纸以逻值为纵坐标对时间(t)作图，则病情进展360百科曲线就成为一条直线，也称逻值线(图中B)。逻值线与纵轴相交的截点，为初始病害数量(x0)，逻值线的斜率就是病害的流行速度，即表观侵染速率。